只计算同 label 之间的节点.
实际上只计算每个连通子图中的紧密中心性.
Wasserman & Faust 算法
该算法是针对于非连通图的变式.
$C_{WF}(u) = \frac{n-1}{N-1}\left(\frac{n-1}{\sum_{v=1}^{n-1}d(u,v)} \right)$
其中:
- $u$ 表示节点.
- $N$ 表示总的节点数量.
- $n$ 表示与 $u$ 在同一个分量中的节点的数量.
- $d(u, v)$ 表示另一个节点 $v$ 到 $u$ 的最短距离.

中介中心性 Betweenness Centrality

用于检测节点对图中信息流或资源的影响程度, 通常用于查找将图的一部分与另一部分桥接的节点.

输入: G = (V, E).
输出: 每个节点及其中介中心值.

实现原理

BC(v) = \sum_{s \neq u \neq t} \frac{\sigma_{st}(v)}{\sigma_{st}}

其中:

$v$ 表示节点.
$\sigma_{st}$ 表示节点 $s$ 和 $t$ 之间最短路径的总和.
$\sigma_{st}(v)$ 表示 $s$ 和 $t$ 之间通过节点 $v$ 的最短路径的数量.

简单来说, 中介中心性就是通过点对之间最短路径通过节点 $v$ 的占比来衡量节点 $v$ 的重要性.

下图中展示了计算中介中间性得分的步骤.

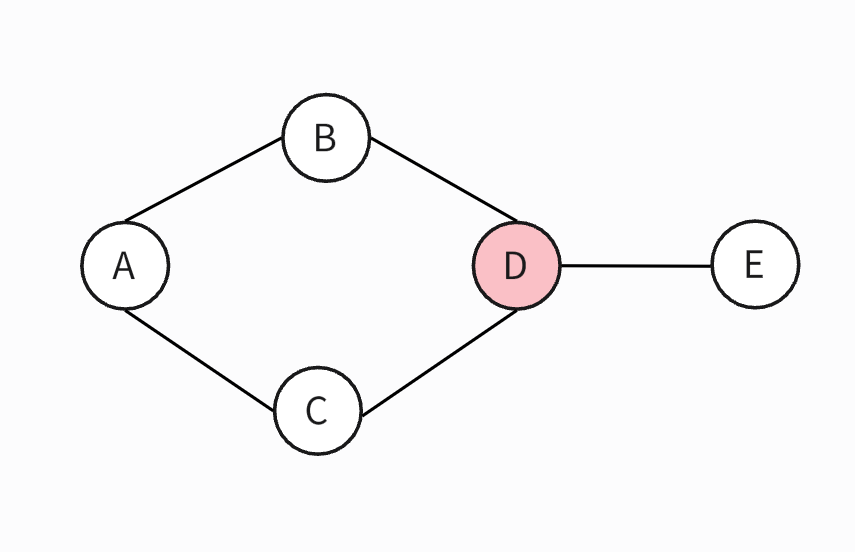
针对节点 D 的计算过程如下:

通过 D 的最短路径节点对	节点对之间的最短路径总数 $p$	占通过 D 最短路径数量的百分比 $\frac{p(u)}{p}$
(A, E)	1	1
(B, E)	1	1
(C, E)	1	1
(B, C)	2 (分别是 B->A->C 和 B->D->C)	0.5

所以根据公式, 节点 D 的中介性得分是: 1 + 1 + 1 + 0.3 = 3.5.

算法步骤

不同于线性的顺序编程计算, 此处给出的算法是基于 Pregel 的消息传播方式进行计算的. 在此仅做参考.

阶段一: 计算出所有点对之间的最短路径以及最短路径数量

初始化
- 对于源节点 $s$ , 路径计数 $\sigma_s = 1$ , 路径长度 $d_s = 0$ .
- 对于其他节点, 路径计数 $\sigma = 0$ , 路径长度 $d = \infty$ .
消息传播
假设节点 $u$ 向节点 $v$ 发送消息.
- 节点 $u$ 消息发送: $(d_u +1, \sigma_u)$ , 即路径长度和路径数量.
- 节点 $v$ $v$ 消息更新:
  - 如果 $d_{new} < d_{current}$ : 更新最短路径长度 $d_v = d_{new}$ , 设置路径数量 $\sigma_v=\sigma_u$ .
  - 如果 $d_{new} = d_{current}$ : 说明找到了另一条等长的路径, 所以增加路径数量 $\sigma_v += \sigma_u$ .

阶段二: 计算每个点的贡献值

contribution = \frac{\sigma_{sv} \times \sigma_{vt}}{\sigma_{st}}

假设我们有三节点：源节点 $s$ , 中介节点 $v$ 和目标节点 $t$ . 我们需要计算的是: 经过节点 $v$ 的路径占从 $s$ 到 $t$ 所有最短路径的比例. 公式中的 $\sigma_{sv} \times \sigma_{vt}$ 就是 $s$ 和 $t$ 之间经过 $v$ 的最短路径数量, 是根据最短路径的组合原理将 $s$ 到 $t$ 的最短路径看作是 $s$ 到 $v$ 和 $v$ 到 $t$ 的路径的组合.

def calculate_betweenness_centrality(source, all_nodes):
    # 初始化源点的中介中心性
    BC_s = 0

    # 遍历所有目标节点 t，t != source
    for t in all_nodes:
        if t == source:
            continue

        # 遍历所有候选节点 v，v != source, v != t
        for v in all_nodes:
            if v == source or v == t:
                continue

            # 获取从 source 到 v 的最短路径数 和 从 v 到 t 的最短路径数
            sigma_sv = get_shortest_path_count(source, v)  # 从source到v的最短路径数
            sigma_vt = get_shortest_path_count(v, t)      # 从v到t的最短路径数
            sigma_st = get_shortest_path_count(source, t) # 从source到t的最短路径数

            # 如果 sigma_st 为 0，表示从 source 到 t 没有最短路径，跳过此对节点
            if sigma_st == 0:
                continue

            # 计算通过 v 的路径数占比
            contribution = (sigma_sv * sigma_vt) / sigma_st

            # 累加贡献到源点的中介中心性
            BC_s += contribution

    return BC_s

对于异质图的适配

该指标计算不涉及属性, 只关注图结构的度.
只计算同 label 下的度.

总结

本文一共介绍了三种不同的中心性算法, 每一种算法都从不同的角度对图中的重要节点进行了衡量.

度中心性算法
通过计算每个节点出入度来对节点的重要性进行评估. 度中心性高的节点意味着与更多的节点有联系.
紧密中心性
通过计算到其他各个节点的平均距离来衡量节点的重要性. 接近中心性高的节点意味着在图中更中心的位置, 从它出发抵达其他所有节点的路径更短, 如果进行消息传播会更快.
中介中心性
通过计算其他节点之间的最短路径通过自身的概率来衡量节点的重要新. 通常用于检测节点对图中信息流或资源的影响程度, 中介中心性高的节点意味着它是图中两团节点之间重要的桥接部分.

本文参考资料