LSM-Tree:一文了解 NoSQL 存储系统的核心的增删查改
如果你曾经接触过 NoSQL 数据库,例如:HBase、LevelDB、RocksDB,那么你应该就听说过 LSM 树。大多数的 NoSQL 数据库的底层都有 LSM 树的身影。LSM 树的概念来自于一篇论文:《The Log-Structured Merge-Tree ( LSM-Tree ) 》,今天我们就来讨论一下 LSM 树的原理以及它是如何增删查改和合并数据的。
原理
首先我们需要明白的是:LSM 树是一种数据结构,它被设计用于处理大量写入操作的场景。但是不要被它的名字所迷惑,它与数据结构中常常提到的二叉树等树结构不同,它并不具有根和叶子节点,也不会涉及到树的分裂和旋转。LSM 树的核心特点是利用顺序写来提高写性能,而稍微牺牲读性能。
主流的 OLAP 数据库 ( 例如:MySQL、postgreSQL、Oracle 等 ) 主要应对的是读大于写的场景,所以在底层数据结构的设计上多采用 B 树或者 B+ 树等树形结构。
LSM 树的思想包括:
- 磁盘顺序写。
- 多个树状结构。
- 冷热数据分级。
- 定期归并。
- 非原地更新。
看不懂没有关系,我们会在下面对其进行一一讲解。
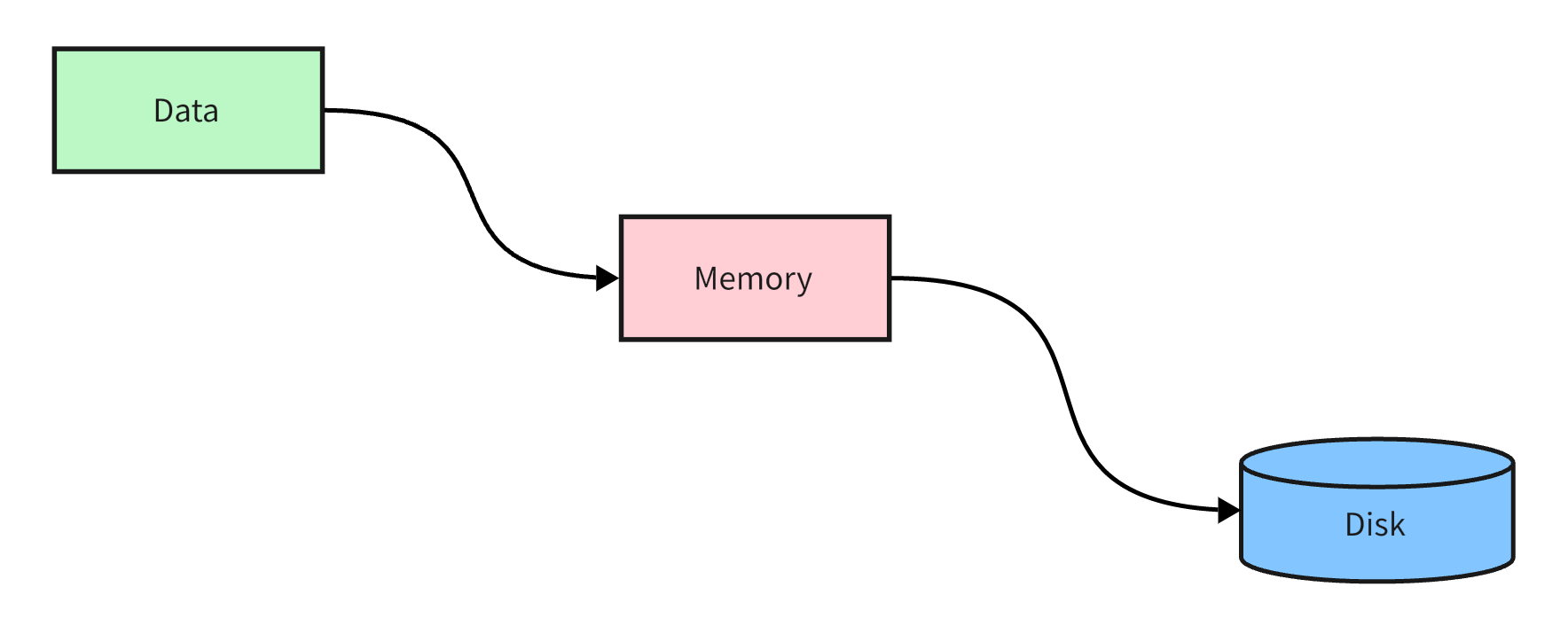
一个存储结构通常来说包含两个部分:内存和磁盘。内存用于热数据的更新,而磁盘则保证数据的持久性。那么当我们的内存随着数据的写入会不断地增大,很显然我们为了保障内存的安全,需要定期地将内存中的数据写入磁盘中,这个操作通常被称为:刷盘。这个时候会遇到 第一个问题:在刷盘的过程中仍然有数据在写入该怎么办?如何处理此时的读写冲突?
读写冲突问题最常见的一个解决方案是:加锁。但是加锁必然带来阻塞的问题,性能上会有一定的影响。LSM 树给出的解决方案是:刷盘开始时将当前内存标记为 只读,重新开辟新的内存空间供客户端写入新的数据。在 LSM 树中,被客户端不断更新的内存空间被称为:Memtable,它通常是一个有序的树状结构,而被置为只读的内存空间被称为:Immutable Memtable。当 Memtable 到达一定大小的时候,就会被转化为 Immutable Memtable,而同时新的写操作会由新的 Memtable 来处理。
解决了读写冲突的问题后,我们注意到:此时 Immutable Memtable 只是被置为了只读模式,但是仍然存在在内存中,还是面临着丢失的风险。所以我们需要将其定期地写到磁盘中,也就是刚刚提到的:刷盘。我们称 Immutable Memtable 保存到磁盘中的文件为:SSTable,而 Immutable Memtable 被保存成 SSTable 的这个过程被称之为:Minor Compaction。
当内存中的数据已经被安全地保存在了磁盘中后,我们开始面临 第二个问题:如何快速查找一个数据? 不同于 MySQL 的 B+ 树索引结构,LSM 树的磁盘部分采用了顺序写的方式,我们该如何在 N 个 SSTable 中查找到我们需要的数据呢?这里就引入了 LSM 树中 层级 和 合并 的概念。
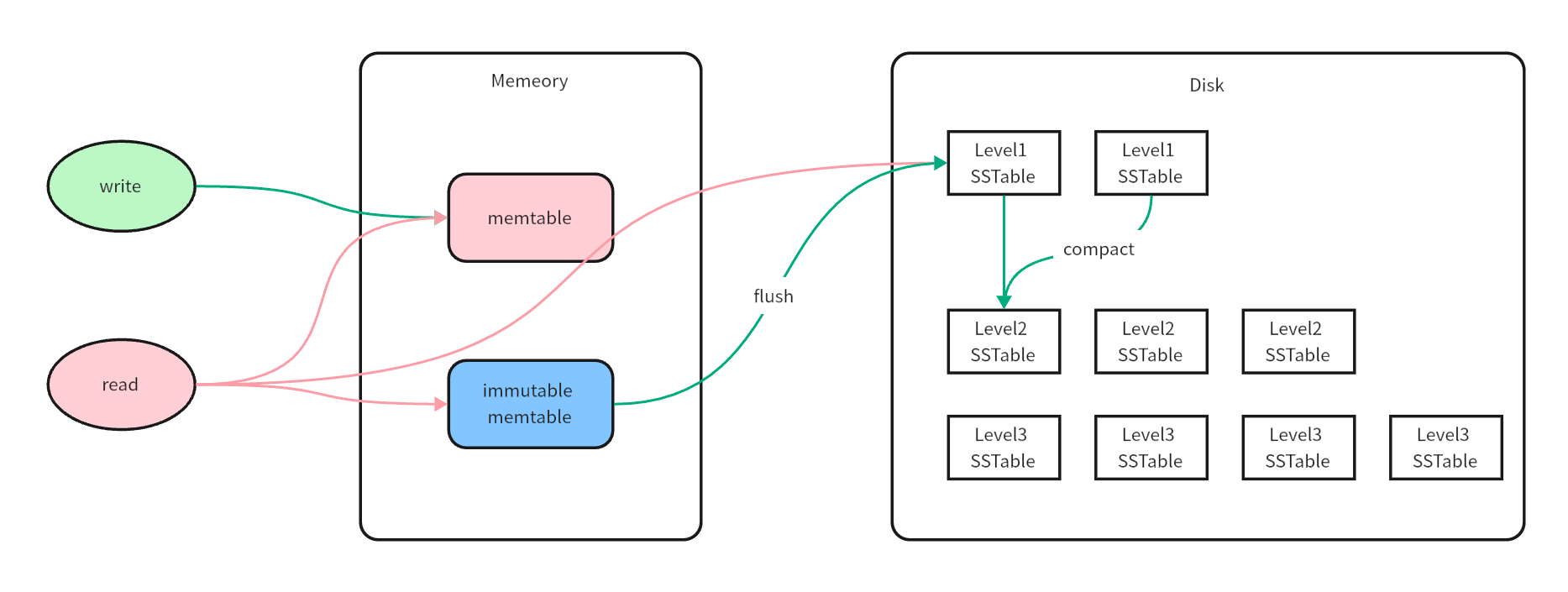
LSM 树将数据分为了不同的层级,其中 Level 0 是内存中的 Memtable,其余的 Level 1 ~ Level n 是不同大小的 SSTable。每个层级中 SSTable 的数量是提前设定好的,通常来说层级越大,所包含的 SSTable 的个数和大小都越大。是的,SSTable 并不是容量相等的数据块,只是同一个层级内的大小相等。当 Level 1 中的 SSTable 个数达到设定的阈值时,就需要将 SSTable 进行有序合并然后将结果写入 Level 2 中去,这也是我们刚刚提到的除了层级的第二个概念:合并。如果你熟悉基础算法的话可以轻易地看出这里使用的算法是多路归并,关于这部分我们在下文中还会提及。
从这个层级的产生和合并的操作中我们可以很容易看出,层级越高的数据越陈旧,层级越低的数据越新。所以我们在查找的时候是从 Level 0 开始查找,即内存中开始查找。如果 Level 0 没有找到,就开始找 Level 1,如果还没有找到就继续查找 Level 2,直至找到目标数据为止。
到此,我们已经简单解释了 LSM 树的一个基础结构:
- Memtable。
- Immutable Memtable。
- SSTable。
如果我们回过头来看前文罗列的 LSM 树的特点,你应该会有更深的体会:
磁盘顺序写。
当数据从内存写入磁盘的时候采用的顺序写的方式。
多个树状结构。
在 Memtable 中采用排序树 ( 红黑树或 AVL 树 ) 等有序的数据结构,而磁盘中的每个 SSTable 都相当于保存了一个树形结构。
冷热数据分级。
热数据在内存中为 Level 0,而冷数据则保存在磁盘中为 Level 1 ~ Level n。
定期归并。
每一层的 SSTable 数量达到阈值时都会触发归并排序的操作对其进行合并,然后将结果写入下一层。
非原地更新。
只有内存中的数据会原地更新,磁盘中的数据都是追加写。
增删查改
在了解了 LSM 树的基础结构后,我们可以来具体看一下这个数据结构是如何完成具体的增删查改的操作的。
插入操作
插入操作非常简单,只需要将数据丢入 Level 0 中即可。Level 0 中通常是一个有序的树形结构,例如:红黑树或 AVL 树。新数据将被插入有序树状结构中合适的位置,这中间可能涉及到树的分裂或旋转。

删除操作
通常删除操作包括两种方式:逻辑删除和物理删除。LSM 树采用的是逻辑删除的方式,通过一种叫:墓碑标记 的特殊数据来标识数据的删除。
删除分为三种情况:
- 待删除的数据在内存中。
- 待删除的数据在磁盘中。
- 待删除的数据不存在。
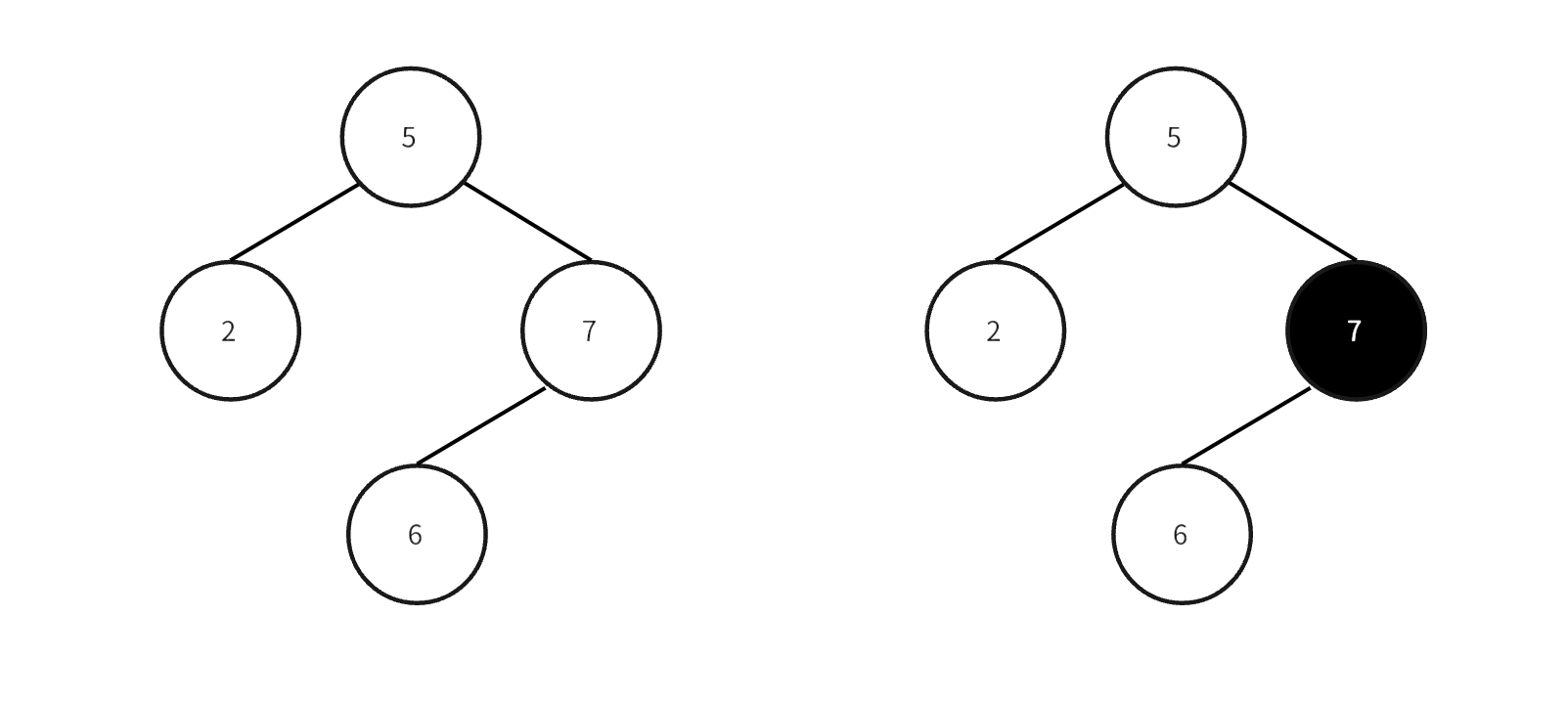
幸运的是,这三种情况的处理方式是一致的:向 Level 0 的树中插入一个对应的墓碑标记。你可以将墓碑标记理解为节点中的一个特殊属性,类似于黑名单。如果数据本身已经在 Level 0 的树中了,则将该节点的墓碑标记置为 1。如果节点本身不在 Level 0 中,即第二和第三种情况,那么就向 Level 0 的树中插入一个墓碑标记已经被置为 1 的一个待删除数据的节点。
修改操作
修改操作和删除操作非常相似,也分为三种情况:
- 待修改的数据在内存中。
- 待修改的数据在磁盘中。
- 待修改的数据不存在。
但是与修改操作不同的是,删除操作不涉及到对数据的覆盖,我们仅仅是进行标记。而 修改操作会涉及到真实的数据覆盖。
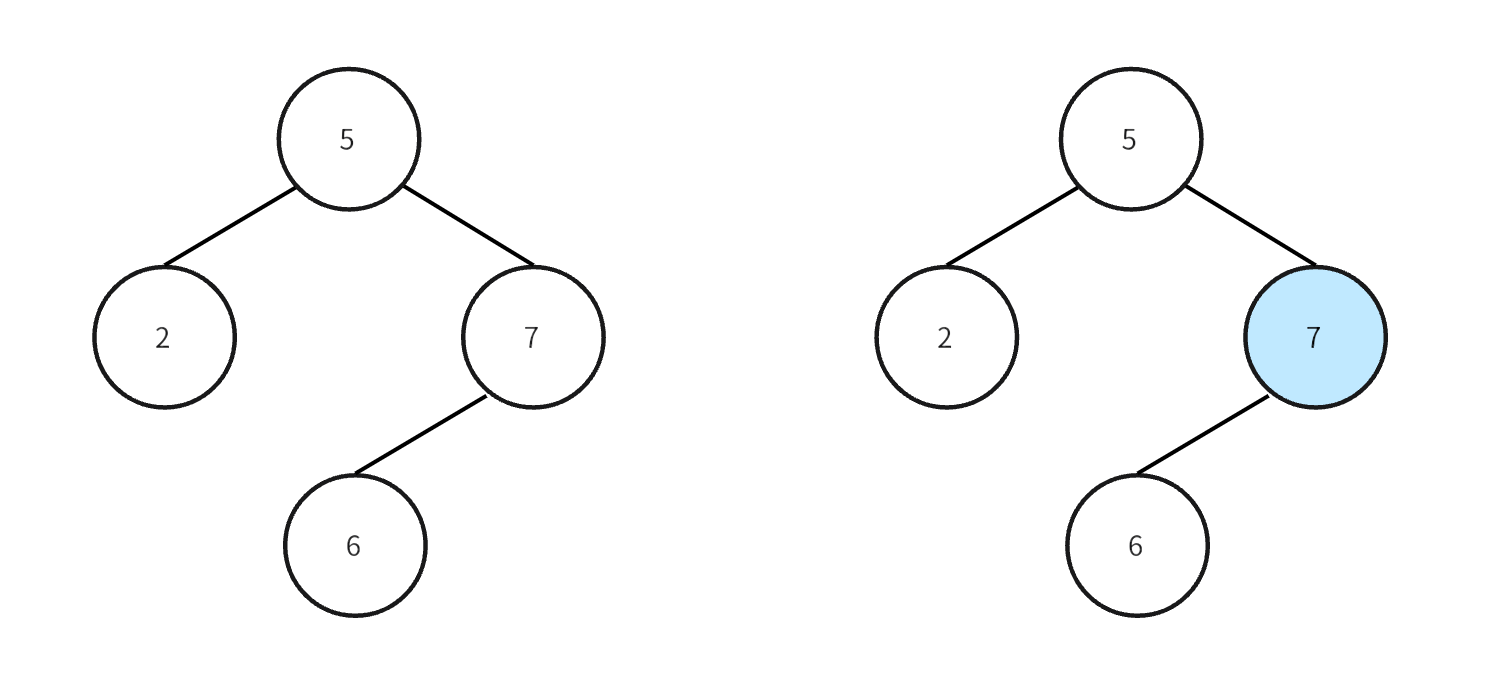
- 待修改的数据在内存中时,直接修改内存中的节点数据。
- 待修改的数据在磁盘中时,在 Level 0 的树中插入一个修改后的新数据。
- 待修改数据不存在时,与第二种情况相同,在 Level 0 的树中插入一个修改后的新数据。
值得一提的是,LSM 树的增加、删除和修改三个操作都只涉及到了在内存中的操作,完全不涉及磁盘的读写。这也是 LSM 树的写性能非常突出的原因之一。
查询操作
我们前面在介绍 LSM 树结构的时候有提到过一点它的查找逻辑:从内存触发,按照顺序查找 Level 0, Level 1, Level 2, Level 3 ... Level n 的每一棵树,一旦匹配则返回。这样的策略保证了我们查找到的一定是最新的数据。
可以很直观地感受到,LSM 树的查询效率相对来说较低。那么有没有什么办法可以提高它的查询效率呢?有的,可以通过布隆过滤器和稀疏索引来进行查询的优化。如果对布隆过滤器不太熟悉的话可以查看我的另一篇博客: 布隆过滤器 ( Bloom Filter ) 的原理及应用 。
合并操作
合并操作是 LSM 树中的核心操作,主要涉及到两个场景:
- Level 0 树达到内存阈值时向磁盘刷盘的时候。
- 磁盘上某一个 Level 的 SSTable 数量达到阈值时,对数据进行归并并向下一个层级写入结果。
内存数据写入磁盘时
对内存中的树进行中序遍历,将数据顺序写入磁盘的 Level 1 层即可。由于 Level 0 中的数据是有序的,所以 Level 1 中的 SSTable 也是有序的。这二者的有序性保证了查询和归并操作时的高效。
多个 SSTable 归并时
当某一层的 SSTable 个数达到阈值时,我们将对多个 SSTable 进行归并,并将结果写入下一个层级。由于每个 SSTable 的内部都是有序的,所以这个过程只涉及到对数据的一次扫描,其时间复杂度为 O ( n ) 。
总结
本文介绍了 LSM 树的结构以及增删查改等基本操作。
由于其对内存的高效利用和对磁盘的追加写策略,LSM 树展现了其吞吐量极大的写操作性能,同时度读操作性能被相对弱化,归并操作也比较消耗资源。
LSM 树遵循的设计原则:
先内存再磁盘。
内存原地更新。
磁盘追加写。
归并保留新值。
LSM 树的增删查改四种操作的时间复杂度分析:
| 操作 | 平均代价 | 最坏代价 |
|---|---|---|
| 插入 | 1 | 1 |
| 删除 | 1 | 1 |
| 修改 | 1 | 1 |
| 查找 | lg(N) | lg(N) |