一种数据挖掘的任务是在图上发现一组频发出现的子结构，这种任务被称为：**频繁子图挖掘 ( frequent subgraph mining ) **。阅读本章需要一定的对于图的基础知识，具体内容可以阅读 [GFD 相关概念解释](/paperNote/9hfux33n/#_4-gfd 相关概念解释) 。

频繁子图挖掘

频繁子图挖掘

给定图的集合 $G$ 和支持度阈值 $minsup$，频繁子图挖掘的目标是找到所有满足 $s ( g ) \geq minsup$ 的子图 $g$。

尽管该定义适用于所有类型的图，但是本节讨论的内容还是聚焦于 无向连通图。

频繁子图挖掘的计算量非常大，复杂性主要来自于两点：

1. 计算给定图 $G$ 的子图 $g$ 的支持度不像项集或序列那样直接，涉及到验证子图和同构图的问题。子图同构问题是 NP-Complete 的。
2. 从一组给定的顶点和边的标签生成的候选子图的数量远多于数据集生成候选项集的数量。

坏消息是由于拓扑结构的引入，暴力枚举的方法已经变得不切实际。但是好消息是，先验原理对于子图仍然适用。所以仍然可以沿用 Apriori 方法的一般结构，将该算法分为 3 个主要步骤：候选生成、候选剪枝和支持度计数。

候选生成

将一对频繁 ( k-1 ) -子图合并成一个候选 k-子图。如果它们共享一个共同的 ( k-2 ) -子图，则称该 ( k-2 ) -子图为 核。当给定一个共同的核，子图合并过程可以描述如下图:

顶点增长策略

边增长策略

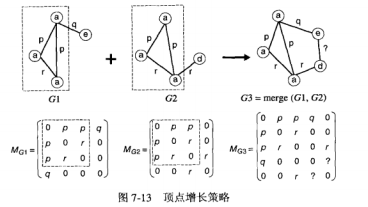
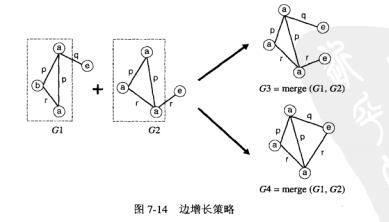
这与前面 第 2 节 中提到的 $F_{k-1} \times F_{1}$ 方法非常相似。

候选剪枝

在产生候选 k-子图后，需要剪去 ( k-1 ) -子图非频繁的候选项。

1. 识别所有可以由从 k-子图删除一条边构建的 ( k-1 ) -子图，并检查它们是否被识别为频繁。
2. 如果其中有任何一个 ( k-1 ) -子图是不频繁的，那么候选 k-子图可以丢弃。
3. 如果两个图是同构的，那么它们的代码相同，因此可以通过比较候选图的规范标签来完成检测并移除重复候选。

支持度计数

维护一个与每个频繁 ( k-1 ) -子图都想关联的图 ID 标。如果新的候选 k-子图通过合并一对频繁 ( k-1 ) -子图生成，就对它们的对应图 ID 表求交集。最后，子图的同构检查就在表中的图上进行。

贡献者

dingyuqi

更新日志

2025/8/5 08:34

查看所有更新日志

• eb6eb-improve(docs): use pangu formatter于 2025/8/5
• 2185e-improve(docs): use chinese punctuation于 2025/3/6
• fea7c-improve(docs): delete extra whitespace and blank lines于 2025/1/21
• c1c02-modify(docs): remanage folders and rename files于 2024/12/17
• 8b943-docs: update docs于 2024/12/2
• d201e-docs: update docs于 2024/11/22
• b63e9-docs: update docs于 2024/11/18
• a5059-整理图片和文章于 2024/11/7
• 114be-整理文章于 2024/11/5
• 4e139-update于 2024/10/17

版权所有

版权归属：dingyuqi

许可证：署名-非商业性-禁止演绎 4.0 国际 (CC-BY-NC-ND-4.0)