当前的大数据中许多数据都是具有固有的序列特征，即事件之间是基于时间或空间的先后次序。例如购物篮数据通常包含商品何时被顾客购买的时间信息。迄今为止，我们在前面的章节中所讨论的关联模式概念都只强调同时出现关系，而忽略数据中的序列信息。对于识别动态系统的重现特征，或者预测特定时间的未来发生，序列信息可能是非常有价值的。

本章将给出序列模式的基本概念和发现序列模式的算法。

预备知识

对象	时间戳	事件
A	10	2,3,5
A	20	1,6
A	23	1
B	11	4,5,6
B	17	2
B	21	1,2,7,8
C	14	1,6
C	28	1,7,8

表 7.1 序列数据举例

1. 序列

   一般地，序列是 元素（事务）的有序列表，记作 $s = <e_1e_2e_3\dots e_n>$，其中每个 $e_j$ 是一个或多个事件的集族。

   例子

   1. web 站点访问者访问 web 页面序列：

   <{首页} {电子产品} {相机和摄像机} {数码项集} {购物车} {订购确认} { 返回购物}>

   2. 计算机专业学生在不同的学期参加课程的序列：

   <{算法与数据结构, 操作系统导论} {数据库系统, 计算机体系结构} {计算机网络, 软件工程} {计算机图形学, 并行程序设计}>

   序列的长度对应序列中的元素个数，包含 k 个事件的序列被称为 k-序列。

2. 子序列。

   若通过删去 $s$ 中的一些事件或者删除 $s$ 中的一些元素能推导出 $t$，则称 $t$ 为 $s$ 的 子序列（subsequence）。形式上讲，如果存在整数 $1 \le j_1<j_2<\dots <j_m \le n$，使得 $t_1 \subseteq s_{j1}, t_2 \subseteq s_{j2}, \dots , t_m \subseteq s_{jm}$，则序列 $t=<t_1t_2\dots t_m>$ 是序列 $s=<s_1s_2\dots s_n>$ 的子序列。如果 $t$ 是 $s$ 的序列，则称 $t$ 包含 在 $s$ 中。

   序列数据 $s$	序列数据 $t$	$t$ 是否为 $s$ 的子序列
   <{2,4}{3,5,6}{8}>	<{2}{3,6}{8}>	是
   <{2,4}{3,5,6}{8}>	<{2}{8}>	是
   <{1,2}{3,4}>	<{1}{2}>	否
   <{2,4}{2,4}{2,5}>	<{2}{4}>	是

   表 7.2 子序列概念例子

序列模式发现

设 $D$ 是包含一个或多个 数据序列（data sequence） 的数据集。数据序列是指与单个数据对象相关联的事件的有序列表。例如 表 5.1 中共有 3 个数据序列，对象 A、B、C 各一个。

序列 $s$ 的支持度是包含 $s$ 的所有数据序列所占的比例。如果序列 $s$ 的支持度大于或等于用户指定的最小支持度阈值，则称 $s$ 是一个序列模式（或频繁序列）。

序列模式发现

给定序列数据集 $D$ 和用户指定的最小支持度阈值 minsup，则序列模式发现的任务是找出支持度大于或等于 minsup 的所有序列。

由于以下的三个原因，相较于候选项集，候选序列的数量是远远多于候选项集的。

1. 一个项在项集中只会出现一次，但是在序列中可能会多次出现。
2. 次序在序列中是重要的，项集和序列的区别相当于组合变排序。
3. 对于序列数据，n 个不同的项的候选项集数量上限为 $2^{n-1}$，但是仅仅 2 个不同事件产生的序列可能数量都相当多。

下面给出类 Apriori 算法从序列数据集中提取序列模式。

序列模式发现的类 Apriori 算法

该算法的结构几乎和前面提到的用于频繁项集发现的 Apriori 算法完全一样。该算法迭代产生新的候选 k-序列，剪掉那些子集中有非频繁 (k-1)-序列的候选，然后对留下的候选计数，识别序列模式。

候选生成

序列的生成和候选项集不同。前面我们通过项集内部的元素使用字典序排序来避免重复产生候选，但是序列本身可能并不符合字典序。合并序列的标准可以用以下过程的形式来表示：

序列 $s^{(1)}$ 与另一个序列 $s^{(2)}$ 合并，仅当从 $s^{(1)}$ 中去掉第一个事件得到的子序列与从 $s^{(2)}$ 中去掉最后一个事件得到的子序列相同。通过如下方式扩展序列 $s^{(1)}$ 来得到候选集：

1. 如果 $s^{(2)}$ 的最后一个元素只有一个事件，则将 $s^{(2)}$ 的最后一个元素合并到 $s^{(1)}$ 的末尾，得到合并后的序列。
2. 如果 $s^{(2)}$ 的最后一个元素多于一个事件，则将 $s^{(2)}$ 的最后一个元素的最后一个事件(不被包含在 $s^{(1)}$ 的最后一个元素)合并到 $s^{(1)}$ 的最后一个元素，得到合并后的序列。

步骤可见下图：

序列模式挖掘算法候选生成和剪枝步骤示例

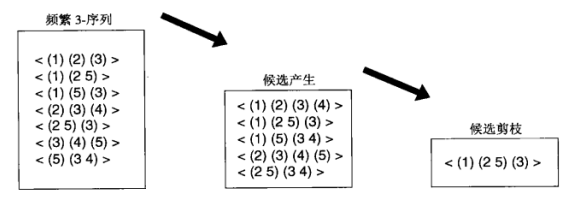
候选剪枝

如果候选 k-序列的 (k-1)-序列至少有一个是非频繁的，那么将它剪掉。

支持度计数

在计算支持度计数期间，算法将识别属于特定数据序列的所有候选 k-序列，并增加其支持度。在对每个数据序列执行该步骤后，算法将识别出频繁 k-序列，并可以丢弃支持度小于最小支持度阈值 minsup 的候选。

贡献者

dingyuqi

更新日志

2025/3/6 08:59

查看所有更新日志

• a1e78-improve(docs): use chinese punctuation于 2025/3/6
• 1289a-improve(docs): delete extra whitespace and blank lines于 2025/1/21
• c2111-modify(docs): remanage folders and rename files于 2024/12/17
• aa2df-docs: update docs于 2024/12/2
• 7577d-docs: update docs于 2024/11/22
• a99ea-docs: update docs于 2024/11/18
• 92ee3-docs: update docs于 2024/11/18

版权所有

版权归属：dingyuqi

许可证：署名-非商业性-禁止演绎 4.0 国际 (CC-BY-NC-ND-4.0)