本节讨论一种重要性质, 该性质对关联分析算法的性能和提取模式的质量具有重要影响. 我们将关注具有倾斜支持度分布的数据集, 其中大多数项具有较低或中等频率, 但是少数项具有很高的频率.

如下图所示, $p$ 是具有 83.8% 的高支持度的项, 而 $q$ 和 $r$ 则是具有 16.7% 的低支持度的项. 尽管 $q$ 和 $r$ 的支持度不高, 但是二者显现出非常强的相关性. 一个模式挖掘算法应当能发现 $\{q,r\}$ 是有趣的.

倾斜支持度数据集

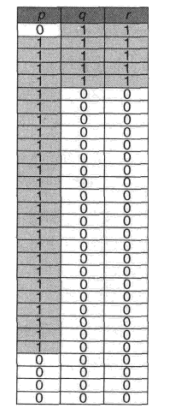
但是很显然为项集 $\{q,r\}$ 选择一个合适的支持度是非常困难的, 如果阈值太高(如 20%), 则可能遗漏涉及类似 $\{q,r\}$ 这种支持度较低的模式. 如果支持度阈值设置太低, 则会使得模式挖掘过程变得过于复杂.

提示

特别地, 可能会提取大量的高频项(如 $p$)和低频率项(如 $q$)相关联的虚假模式, 这样的模式就是所谓的交叉支持模式(cross-support).

这是由于 $p$ 和 $q$ 之间的关联性大部分都是受 $p$ 项的频率发生而不是 $p$ 和 $q$ 共同出现的影响. 由于 $\{p,q\}$ 的支持度和 $\{q,r\}$ 的支持度非常接近, 当为了挖掘 $\{q,r\}$ 而将支持度设置较低时, 很自然地 $\{p,q\}$ 也会被选择出来.

交叉支持模式

交叉支持模式是一个项集 $X=\{i_1,i_2,\dots, i_k\}$, 它的支持度比率

$$\tag{6.1} r(X)=\frac{min\left[ s(i_1), s(i_2), \dots, s(i_k) \right]}{max\left[ s(i_1), s(i_2), \dots, s(i_k) \right]}$$

小于用户指定的阈值 $h_c$.

很遗憾的是现有的度量都不足以消除交叉支持模式. 不过这不代表我们什么都做不了.

虽然 $\{p\}\rightarrow \{q\}$ 的置信度非常低, 但是 $\{r\}\rightarrow \{q\}$ 的置信度很高. 通过这一观察, 可以通过从给定项集提取出的最低置信度规则来检测交叉支持模式. 使用下面的方法可以找到最低置信度规则:

1. 前面章节中提到的置信度的反单调性:

   $$\tag{6.2} conf(\{i_1i_2\}\rightarrow \{i_3,i_4,\dots, i_k\}) \le conf(\{i_1i_2i_3\}\rightarrow \{i_4,\dots, i_k\})$$

   该性质表明, 把关联规则左边的项不断一道右边之后不会增加规则的置信度. 根据这个性质可以知道, 一个频繁项集中置信度最低的规则是左边仅包含一个项的规则, 我们用 $R_1$ 表示.

2. 规定一个频繁项集 $\{i_1,i_2,\dots,i_k\}$, 如果 $s(i_j)=max\left[ s(i_1), s(i_2), \dots, s(i_k) \right]$, 则规则

   $$\tag{6.3} \{i_j\}\rightarrow \{i_1,i_2,\dots, i_{j-1},i_{j+1}, \dots,i_k\}$$

   是 $R_1$ 中具有最小置信度的规则.

3. 所以, 可以从频繁项集 $\{i_1,i_2,\dots,i_k\}$ 中得到的最低置信度为:

   $$\tag{6.4} \frac{ s(\{i_1,i_2,\dots,i_k\})}{max\left[ s(i_1), s(i_2), \dots, s(i_k) \right]}$$

   该表达式也被称为h置信度(h-confidence)或全置信度(all-confidence). 由于支持度的单调性, 所以我们又能知道:

   $$\tag{6.5} h\text{-}confidence(X)\le \frac{min\left[ s(i_1), s(i_2), \dots, s(i_k) \right]}{max\left[ s(i_1), s(i_2), \dots, s(i_k) \right]}$$

   我们可以看到 公式(6.5) 和 公式（6.1）是一样的.

那么 h-confidence 是如何帮助我们消除交叉支持模式的呢? 由于交叉支持模式的支持度比率总是小于 $h_c$, 所以这类模式的 h-confidence 也一定小于 $h_c$. 所以, 通过确保模式的 h-confidece 大于 $h_c$ 即可消除交叉支持模式. 最后值得一提的是: 使用 h-confidence 的好处不仅仅是能消除交叉支持模式, 这种度量也是反单调的, 即:

$$\tag{6.6} h\text{-}confidece(\{i_1,i_2,\dots,i_k\})\ge h\text{-}confidece(\{i_1,i_2,\dots,i_{k+1}\})$$

从而可以将其并入挖掘算法. 此外, h-confidence 可以确保项集中的项之间是强关联的. 例如, 假定一个项集 $X$ 的 h-confidence 是 80%. 如果 $X$ 的一个项出现在某事务中, 则 $X$ 中其他的项至少有 80% 的概率属于同一个事务. 这种强关联模式又被称为超团模式(hyperclique pattern).

超团模式

给定项集 $X$, 如果 $h\text{-}confidence(X) > h_c$, 则称 $X$ 为超团模式, 其中 $h_c$ 表示用户定义的阈值.

贡献者

• dingyuqi

变更历史

最后更新于: 查看全部变更历史

• HEAD -> main于 2024/11/22
• 92ee3-

  docs: update docs

  于 2024/11/18