令 是一个项集, 是项集的一个子集。如果规则 不满足置信度阈值,则形如 的规则一定也不满足执行都阈值。其中 是 的子集。
规则的产生和频繁项集的紧凑表示
约 1199 字大约 4 分钟
2024-05-27
在 上一节 中我们结束了频繁项集的产生的内容。本节将讲述如何使用计算产生的频繁项集来产生规则。
规则的产生
由于每个频繁 k-项集都能够产生多达 2k−2 个规则 ( 忽略那些前件或后件为空的规则,如:∅→Y 或 Y→∅ ) ,所以我们需要一个有效的方法从频繁项集中提取出所有的规则。
我们可以这样做:将项集 Y 划分成两个非空的子集 X 和 Y−X,使得 X→Y−X 满足置信度阈值。
提示
这样的规则必然满足支持度阈值,因为他们是由频繁项集产生的。
基于置信度的剪枝
置信度不具备像支持度度量那样的反单调性。尽管如此,当比较由频繁项集 Y 产生的规则时,下面的定理对置信度度量成立:
定理 4.1 的证明
考虑如下的两个规则:X~→Y−X~ 和 X→Y−X,其中 X~⊂X。这两个规则的置信度分别为 σ(X~)σ(Y) 和 σ(X)σ(Y)。由于 X~ 是 X 的子集,所以 σ(X~)≥σ(X)。因此,前一个规则的置信度不可能比后一个规则的更大。
Apriori 算法中规则的产生
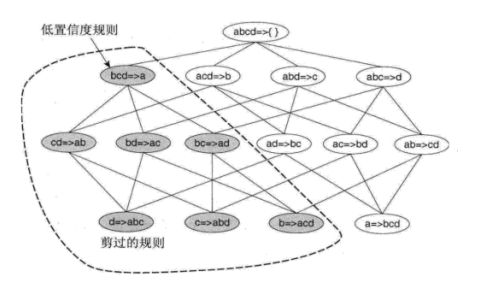
Apriori 算法使用一种逐层的方法来产生关联规则,其中每层对应于规则后件中的项数,如下图。根据上面提到的 定理 4.1,如果格中任意节点具有低置信度,则可以立即剪掉该节点生成的整个子图。
频繁项集的紧凑表示
在实际的应用中,频繁项集的数量可能非常巨大。因此要从中识别出可以推导出其他所有的频繁项集的、较小的、具有代表性的项集是很有必要的。现在介绍两种具有代表性的项集:极大频繁项集和闭频繁项集。
极大频繁项集
若频繁项集的直接超集都不是频繁的,则它是极大频繁项集。
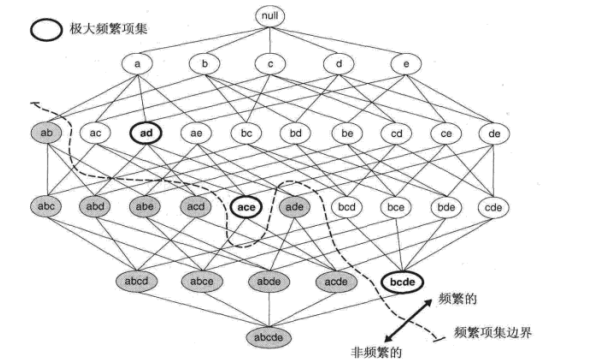
图中的虚线表示频繁项集的边界。虚线上方的项集都是频繁的,下方的都是非频繁的。很显然 {a,d}, {a,c,e} 和 {b,c,d,e} 都是极大频繁集,因为它们的所有直接超集都是非频繁的。而 {a,c} 则因为有一个直接超集 {a,c,e} 不是频繁的,所以它不是最大频繁项集。
极大频繁项集有效地提供了频繁项集的紧凑表示。也就是说,极大频繁项集形成了可以导出所有频繁项集的最小的项集的集合。
但是该种表示法也有缺点。尽管提供了一种紧凑的表示,但是极大频繁项集并不包含它们子集的支持度信息。因此,这就需要再次扫描数据集,来确定那些非极大的频繁项集的支持度计数。
闭项集
闭项集提供了一种所有频繁项集的最小表示,该表示不会丢失支持度信息。
如果项集 X 的直接超集都不具有和它相同的支持度计数,则该项集是闭项集。
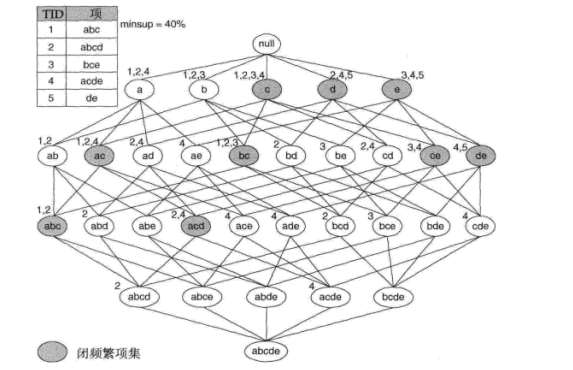
可以从图中看到,每个包含 b 的项都包含 c,所以 b 和 bc 两个项集的支持度都为 3 ( TID = 1,2,3 的三个项 ) 。因此 b 不是闭项集。
闭项集的性质导致了如果知道了它们的支持度计数,就可以由此得到项集格中的每个其他项集的支持度计数。
如果一个项集是闭的,并且其支持度大于或等于最小支持度阈值,那么该项集是闭频繁项集。
在上图中的例子,加入支持度阈值为 40%,那么项集 {b,c} 是闭频繁项集,因为它的支持度是 60%。
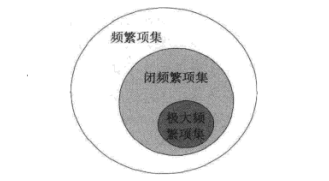
最后,请注意这三种概念的关系:
贡献者
更新日志
941fa-feat(theme): upgrade and use collections于eb6eb-improve(docs): use pangu formatter于2185e-improve(docs): use chinese punctuation于fea7c-improve(docs): delete extra whitespace and blank lines于c1c02-modify(docs): remanage folders and rename files于d201e-docs: update docs于b63e9-docs: update docs于a5059-整理图片和文章于114be-整理文章于fc266-整理图片格式和名称(not finished)于