How Bloom Filters work

About 852 wordsAbout 3 min

2024-12-18

Bloom filters are a probabilistic data structure that checks for presence of an item in a set.

Use Scenarios

The main use scenario of Bloom filter is to quickly determine whether an element is in a set. It is usually used to filter massive data requests and improve the efficiency of data search. For example, when watching Douyin, if you want to determine whether the video has been collected by the current user, it is a question of determining whether an element is in a set. We can use Bloom filter to improve the efficiency of query.

Basic Principle

Bloom filter is a probabilistic data structure with space advantage. The core is a super large bit array and hash function, which is used to answer the question of whether an element exists in a set, but there may be misjudgment-that is, an element is not in the set but is considered to be in the set.

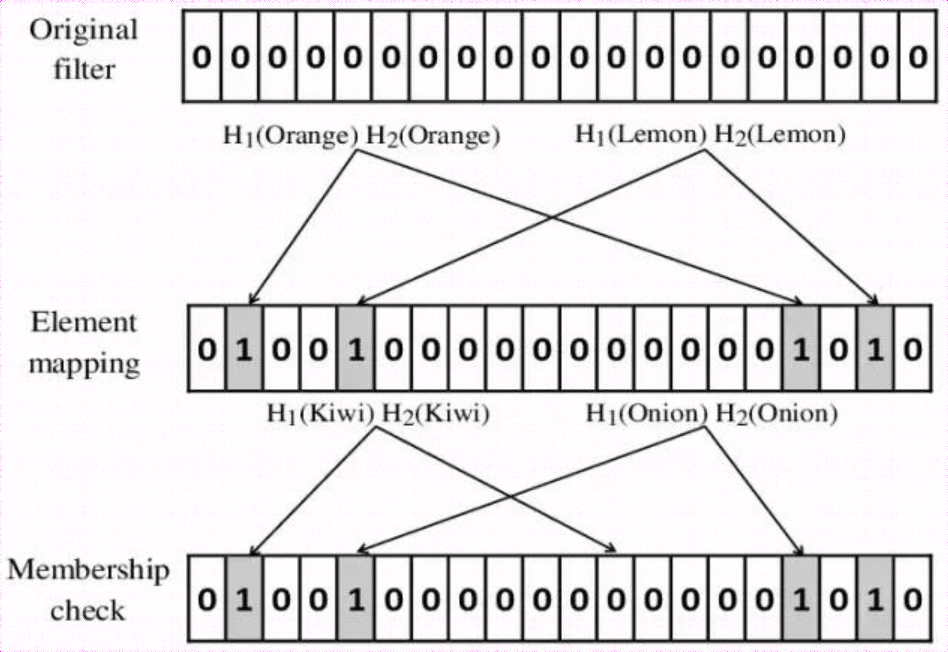
Given a hash space of length N bits.
Select d hash functions, each of which maps a given element to [0, N-1], and set that position to 1.
Use the d hash functions in 2 to calculate the d positions of the element to be judged, $a_1, a_2, \dots, a_d$ .
If one of the corresponding bits of $a_1, a_2, \dots, a_d$ is not 1, then the element is definitely not in the set.
If the corresponding bits of $a_1, a_2, \dots, a_d$ are all 1, then the element may exist in the set.

Parameters

From the above, it can be seen that a Bloom filter should have at least the following parameters:

The size of the hash space, denoted as $m$ . In the above example, $m$ = 20 bits.
The size of the element set, denoted as $n$ . In the above example, $n$ = 2.
The number of hash functions, denoted as $k$ . In the above example, $k$ = 2.
Because BF allows errors, an element may not be in the set but is mistakenly judged to be in the set. The probability of this mistake is called false positive, denoted as $\varepsilon$ .

When the error rate is the smallest, the relationship between the parameters is as follows:

k = \frac{m}{n} \ln2

m = - \frac{n \ln \epsilon}{(\ln 2)^2}

\frac{m}{n}=- \frac{\log_2 \epsilon}{\ln 2} \approx -1.44 \log_2 \epsilon

How To Choose A Hash Function?

From the perspective of probability calculation and speed, the hash function must meet the following requirements:

Independent and uniformly distributed.
Fast calculation speed.

Here we recommend to learn about the murmur algorithm

Advantages And Disadvantages

Advantages

High memory efficiency.
Fast query speed.
Parallel processing.

Disadvantages

There is a false positive rate. It mainly depends on the number of hash functions and the size of the bit array. A larger bit array can reduce the false positive rate, but it will increase memory consumption, so a trade-off is needed.
There is a hash conflict.
Deletion is not supported.
The original data cannot be obtained.

Application

Database prevents database penetration. Use BloomFilter to reduce disk searches for non-existent rows or columns. Avoiding costly disk searches will greatly improve the performance of database query operations.
Determine whether a user has read a video or article in a business scenario. For example, Douyin or Toutiao.

Demo

In Go language, we can use the following package to easily implement a Bloom filter.

main.go

package main

import (
"fmt"
"github.com/bits-and-blooms/bloom"
)

func main(){
m, k := bloom.EstimateParameters(uint(len(md)), 0.001)
filter := bloom.New(m, k)
for d := range md {
if len(d) == 0 {
continue
}
filter.Add([]byte(d))
}
if filter.Test([]byte(d)) {
fmt.print("data already exist!")
}
}

Performance Comparison

Input data size 0.01	Bloom memory/CPU peak	Map memory/CPU peak	Memory savings
1w	0.8MB	1.18MB	32.5%
5w	1.5MB	3.3MB	54.5%
10w	1.37MB	3.66MB	62%
50w	2.24MB	23.2MB	90%
100w	2.7MB	46.1MB	94%
500w	9.3MB	191.4MB	95%
1000w	17.6MB	382.5MB	95%
5000w	61.7MB	1705.2MB	96%

Memory usage Bloom reduction 60% - 90% memory usage

Input data volume 0.01	Bloom query time	Map query time	Time increase
1w	1+1=2ms	508+508=1ms	200%
5w	5.6+4.8=10.5ms	3.2+3.0=6.3ms	166%
10w	12+9.6=21.8ms	9+6=15ms	145%
50w	61.1+52.1=113.2ms	51.6+47.6=99.1ms	114%
100w	125.9+109.4=235.3ms	136.5+121.5=258ms	91%
500w	665.5+592=1.26s	723.5+711.8=1.4s	90%
1000w	1.87+1.5=3.9s	1.48+1.4=2.9s	134%
3000w	16.5s	9.8s	168%
5000w	15+13=28s	7.6+7.6=15.2s	184%