If you have ever been exposed to NoSQL databases, such as HBase, LevelDB, and RocksDB, then you should have heard of LSM trees. Most NoSQL databases have LSM trees at the bottom. The concept of LSM trees comes from a paper: The Log-Structured Merge-Tree (LSM-Tree). Today we will discuss the principles of LSM trees and how they add, delete, query, modify and merge data.

Quick link: The Log-Structured Merge-Tree (LSM-Tree)

Principle

First of all, we need to understand that LSM tree is a data structure designed to handle scenarios with a large number of write operations. But don't be confused by its name. It is different from tree structures such as binary trees that are often mentioned in data structures. It does not have root and leaf nodes, and does not involve tree splitting and rotation. The core feature of LSM tree is to use sequential writing to improve write performance, while slightly sacrificing read performance.

Mainstream OLAP databases (such as MySQL, postgreSQL, Oracle, etc.) mainly deal with scenarios where reads are greater than writes, so the design of the underlying data structure mostly uses tree structures such as B-tree or B+ tree.

The ideas of LSM tree include:

• Disk sequential writing.
• Multiple tree structures.
• Hot and cold data classification.
• Periodic merging.
• Non-in-place updates.

It doesn't matter if you don't understand, we will explain them one by one below.

A storage structure usually consists of two parts: memory and disk. Memory is used to update hot data, while disk ensures data persistence. Then when our memory continues to increase with the writing of data, it is obvious that in order to ensure the security of memory, we need to regularly write the data in memory to disk. This operation is usually called: flushing disk. At this time, we will encounter ==The first problem: What should I do if there is still data being written during the flushing process? How to deal with the read-write conflict at this time? ==

Storage structures usually include memory and disk

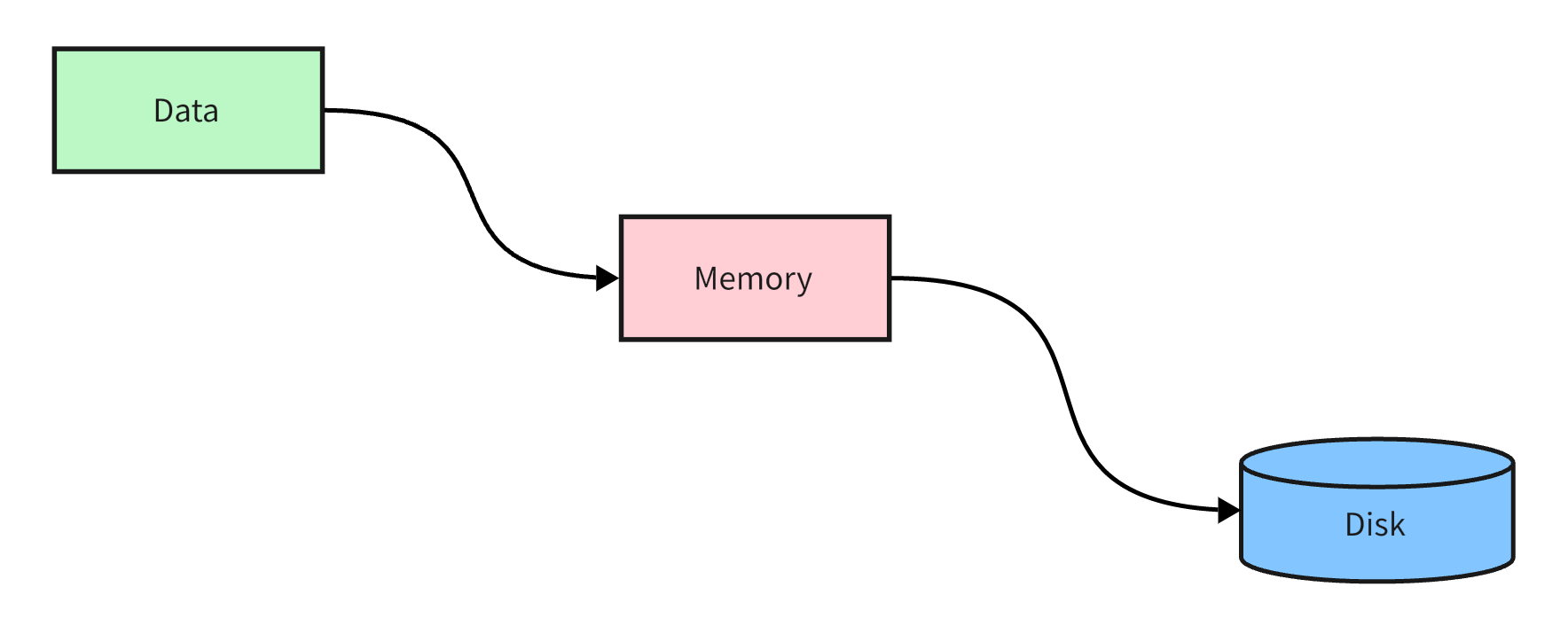
The most common solution to the read-write conflict problem is: locking. However, locking will inevitably bring about blocking problems, which will have a certain impact on performance. The solution given by the LSM tree is: mark the current memory as read-only at the beginning of the flush, and re-open new memory space for the client to write new data. In the LSM tree, the memory space that is constantly updated by the client is called: Memtable, which is usually an ordered tree structure, and the memory space that is set to read-only is called: Immutable Memtable. When the Memtable reaches a certain size, it will be converted to Immutable Memtable, and at the same time, new write operations will be handled by the new Memtable.

After solving the problem of read-write conflicts, we noticed that: at this time, the Immutable Memtable is only set to read-only mode, but it still exists in memory and is still facing the risk of loss. So we need to write it to the disk regularly, which is just mentioned: flushing the disk. We call the file saved by Immutable Memtable to disk: SSTable, and the process of saving Immutable Memtable to SSTable is called: Minor Compaction.

After the data in memory has been safely saved on the disk, we begin to face ==The second problem: how to quickly find a data? == Unlike MySQL's B+ tree index structure, the disk part of the LSM tree uses a sequential write method. How can we find the data we need in N SSTables? Here we introduce the concepts of level and merge in the LSM tree.

LSM tree architecture diagram

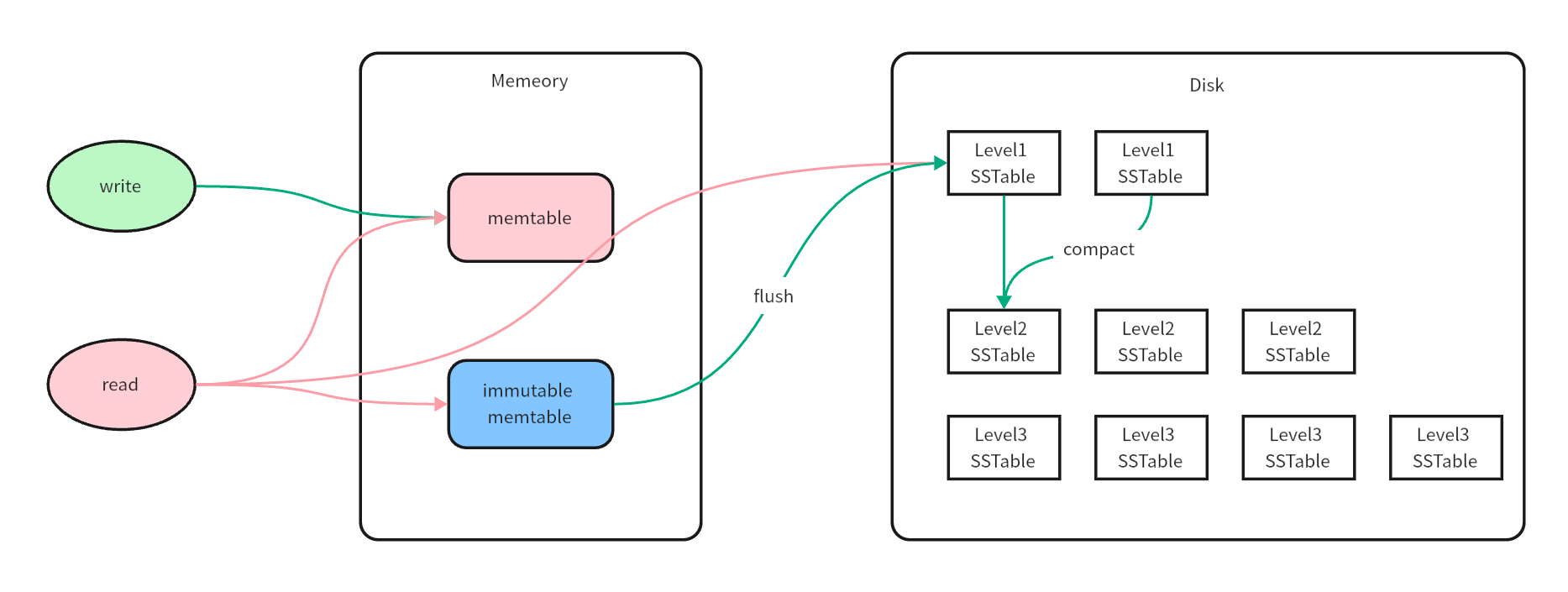
LSM tree divides data into different levels, where Level 0 is the Memtable in memory, and the rest of Level 1 ~ Level n are SSTables of different sizes. The number of SSTables in each level is set in advance. Generally speaking, the larger the level, the larger the number and size of the SSTables it contains. Yes, SSTables are not data blocks with equal capacity, but the sizes within the same level are equal. When the number of SSTables in Level 1 reaches the set threshold, the SSTables need to be merged in order and the results written to Level 2. This is the second concept we just mentioned besides the level: merge. If you are familiar with the basic algorithm, you can easily see that the algorithm used here is multi-way merging, which we will mention later.

From the generation and merging operations of this level, we can easily see that the higher the level, the older the data, and the lower the level, the newer the data. So when we search, we start from Level 0, that is, we start searching in memory. If Level 0 is not found, we start looking for Level 1. If it is still not found, we continue to search for Level 2 until the target data is found.

So far, we have briefly explained a basic structure of the LSM tree:

• Memtable.
• Immutable Memtable.
• SSTable.

If we look back at the characteristics of the LSM tree listed in the previous article, you should have a deeper understanding:

• Disk sequential write.

  The sequential write method used when data is written from memory to disk.

• Multiple tree structures.

  In Memtable, an ordered data structure such as a sorted tree (red-black tree or AVL tree) is used, and each SSTable in the disk is equivalent to storing a tree structure.

• Hot and cold data are graded.

  Hot data is Level 0 in memory, while cold data is stored in disk as Level 1 ~ Level n.

• Periodic merging.

  When the number of SSTables in each layer reaches the threshold, a merge sort operation will be triggered to merge them, and then the result will be written to the next layer.

• Non-in-place updates.

  Only the data in the memory will be updated in-place, and the data in the disk will be appended.

CRUD

After understanding the basic structure of the LSM tree, we can take a closer look at how this data structure completes the specific operations of adding, deleting, querying and modifying.

Insertion Operation

The insertion operation is very simple, just throw the data into Level 0. Level 0 is usually an ordered tree structure, such as a red-black tree or an AVL tree. New data will be inserted into the appropriate position in the ordered tree structure, which may involve splitting or rotating the tree.

Insert a new value into the LSM tree: 6

Delete Operation

Usually, there are two ways to delete: logical deletion and physical deletion. The LSM tree uses logical deletion, and uses a special data called tombstone to mark the deletion of data.

There are three cases of deletion:

1. The data to be deleted is in memory.
2. The data to be deleted is on disk.
3. The data to be deleted does not exist.

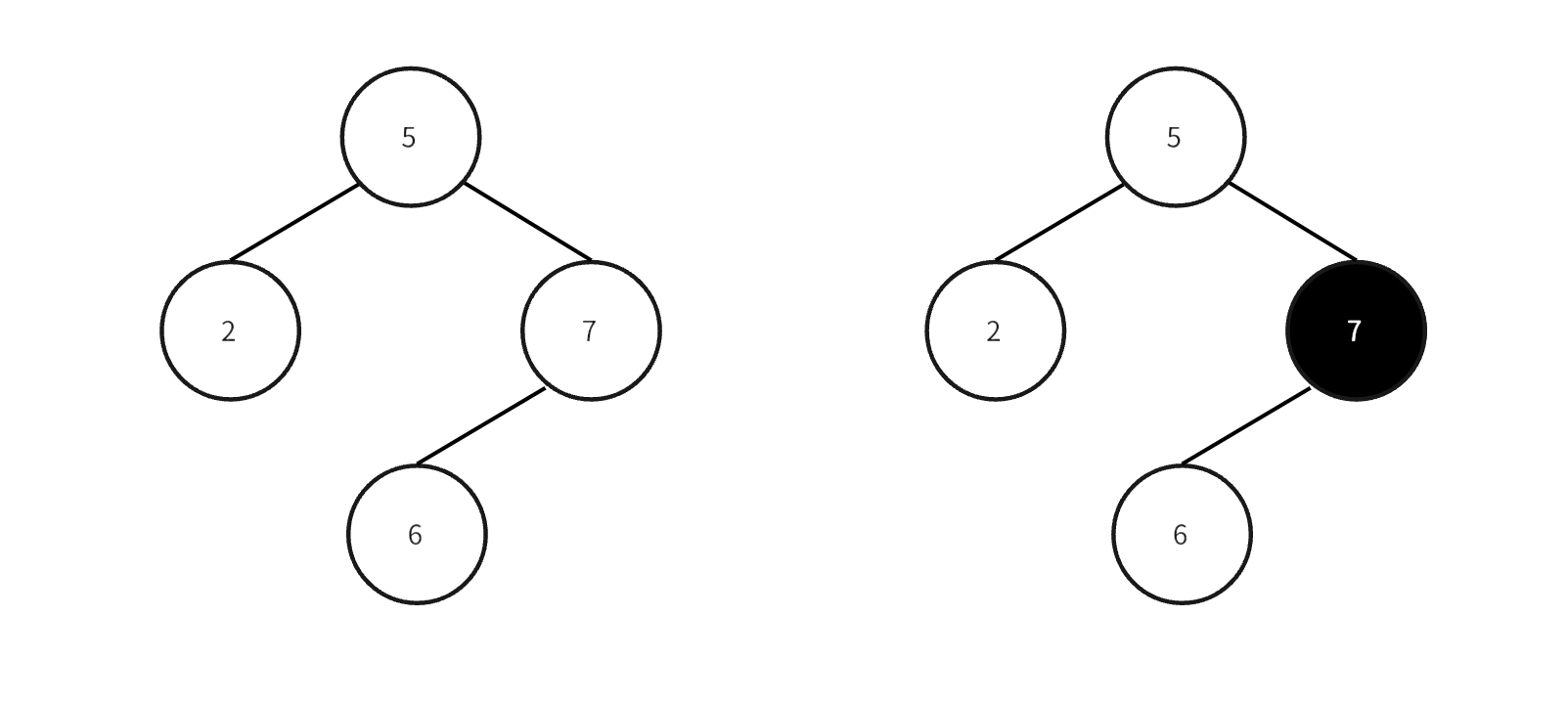
Fortunately, the processing method for these three cases is the same: insert a corresponding tombstone marker into the Level 0 tree. You can understand the tombstone marker as a special attribute in the node, similar to a blacklist. If the data itself is already in the Level 0 tree, set the tombstone marker of the node to 1. If the node itself is not in Level 0, that is, the second and third cases, then insert a node with the data to be deleted and the tombstone mark set to 1 into the tree of Level 0.

Delete a value from the LSM tree: 7

Modification Operation

The modification operation is very similar to the deletion operation, and is also divided into three cases:

1. The data to be modified is in memory.
2. The data to be modified is on disk.
3. The data to be modified does not exist.

However, unlike the modification operation, the deletion operation does not involve overwriting the data, we only mark it. And the modification operation involves real data overwriting.

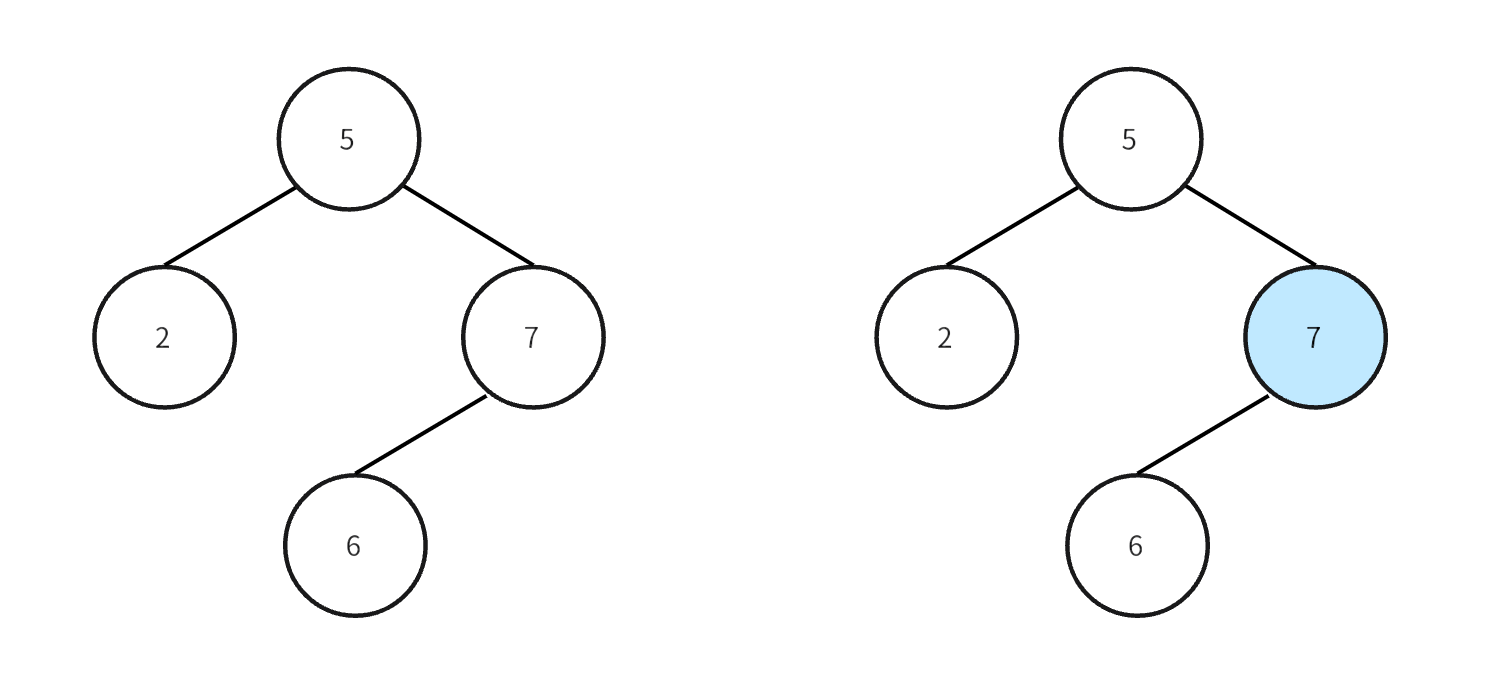
1. When the data to be modified is in memory, directly modify the node data in memory.
2. When the data to be modified is on disk, insert a modified new data into the tree of Level 0.
3. When the data to be modified does not exist, insert a modified new data into the tree at Level 0, just like the second case.

Modify a value from the LSM tree: 7

It is worth mentioning that the three operations of adding, deleting and modifying the LSM tree only involve operations in memory, and do not involve disk reading and writing at all. This is one of the reasons why the write performance of the LSM tree is very outstanding.

Query Operation

When we introduced the LSM tree structure earlier, we mentioned its search logic: trigger from memory, search each tree of Level 0, Level 1, Level 2, Level 3 ... Level n in order, and return once a match is found. This strategy ensures that we must find the latest data.

It can be intuitively felt that the query efficiency of the LSM tree is relatively low. So is there any way to improve its query efficiency? Yes, you can use Bloom filters and sparse indexes to optimize queries. If you are not familiar with Bloom filter, you can check out my other blog: Principle and Application of Bloom Filter.

Merge Operation

Merge operation is the core operation in LSM tree, which mainly involves two scenarios:

1. When the Level 0 tree reaches the memory threshold and flushes to disk.
2. When the number of SSTables at a certain level on disk reaches the threshold, merge the data and write the results to the next level.

When writing memory data to disk

Perform in-order traversal of the tree in memory and write the data sequentially to the Level 1 layer of the disk. Since the data in Level 0 is ordered, the SSTables in Level 1 are also ordered. The orderliness of these two ensures the efficiency of query and merge operations.

When merging multiple SSTables

When the number of SSTables at a certain level reaches the threshold, we will merge multiple SSTables and write the results to the next level. Since each SSTable is ordered internally, this process only involves one scan of the data, and its time complexity is O(n).

Summary

This article introduces the structure of the LSM tree and basic operations such as addition, deletion, query, and modification.

• Due to its efficient use of memory and disk append write strategy, the LSM tree shows its extremely high throughput write operation performance, while the read operation performance is relatively weakened, and the merge operation is also more resource-intensive.

• The design principles followed by the LSM tree are:

  • Memory first, then disk.
  • Memory is updated in place.
  • Disk append write.
  • Merge to retain new values.

• Time complexity analysis of the four operations of adding, deleting, checking and modifying LSM trees:

Operation	Average cost	Worst cost
Insert	1	1
Delete	1	1
Modify	1	1
Search	$lg(N)$	$lg(N)$

References for this article

1. In-depth and simple analysis of LSM tree (log structure merge tree)
2. Asking questions to yourself like crazy - analyzing LSM Principle

Contributors

dingyuqi

Changelog

4/3/25, 8:45 AM

View All Changelog

• 29528-feat(docs): add a new english articleon 4/3/25

Copyright

Copyright Ownership:dingyuqi

License under:Attribution-NonCommercial-NoDerivatives 4.0 International (CC-BY-NC-ND-4.0)