摘要以及相关概念

约 2041 字大约 7 分钟

2023-10-31

论文原文：Discovering Graph Functional Dependencies。

其中涉及到的一些非常重要的基本概念，在 Functional Dependencies for Graphs 论文中有详细阐述。

本论文是樊文飞院士图计算理论中非常重要的一环，也是钓鱼城数据挖掘系统的主要参考论文之一。接下来我将提取该论文中的主要论点和推理，并结合实际的工程实现和项目经验（应该会单独写一篇博客）阐述个人一部分的理解。中间有理解不到位的地方，希望各位大佬及时指正。

本章节会对论文的工作和基础概念进行梳理，会有部分内容是论文的翻译，我会对翻译部分和我自己的理解部分分别进行标识。翻译部分如果有表达不通顺的地方，请大家谅解。

摘要翻译

本文研究了 GFDs 的发现，GFDs 是一类在图上定义的函数依赖关系。我们研究了与 GFD 发现相关的三个基本问题的固定参数的可处理性。我们表明，隐含和满足性问题是固定参数的，但验证问题是 co-W 困难的。我们引入了减少 GFD（reduced GFD）及其拓扑支持度的概念，并形式化了 GFD 的发现问题。我们开发了用于发现 GFD 并计算其集合（covers）的算法。此外，我们通过提供用于发现 GFD 的并行可扩展算法来证明 GFD 发现在大规模图上是可行的，这些算法保证在使用更多处理器时减少运行时间。使用现实生活和合成数据，我们通过实验验证了算法的有效性和可扩展性。

关键词: GFD 发现，并行扫描，固定参数易解性

文章的主要贡献以及相关工作

贡献

研究了三个 GFD 挖掘相关的基础问题。
1. 满足性问题。决定 GFDs 是否是"脏"的，即 GFDs 有一个模型。
2. 蕴含问题。决定 GFD 挖掘是否是"多余的"。
3. 验证性问题。是为了确保从图 G 中挖掘的 GFD 满足 G。
形式化了 GFDs 的挖掘过程。
开发了一个时间顺序的 GFDs 的挖掘算法。
我们开发了一种并行算法，用于在分裂的图中发现 GFDs。
使用生活中的数据和构造数据，我们评估了算法。

挖掘目标

我们先来看一下，通过算法我们最终会得到一个什么样的结果以及这个结果有什么含义。

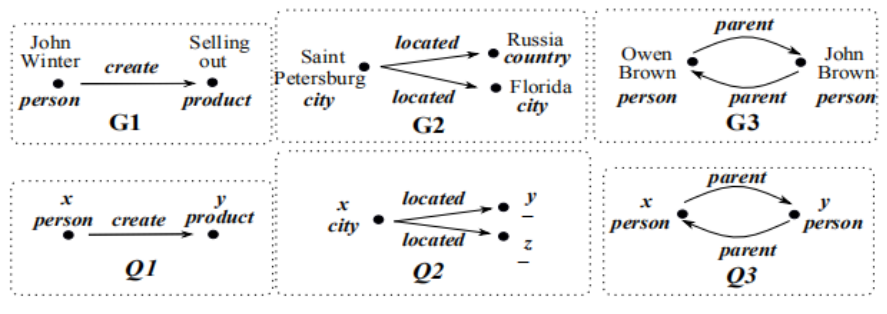
上面是 3 个论文中给出的 GFD 的例子，其中 $\varphi1, \varphi2, \varphi3$ 就是我们最后算法得到的结果。

GFD $\varphi1 = Q_1[x,y](y.type=''film'' \rightarrow x.type=''producer'')$ 。其中 $Q_1$ 在图中已经展示， $x$ 和 $y$ 是两个变量表示 $Q_1$ 中的两个点，每个点拥有一个属性 $type$ （图中并没有显示）。 $\varphi1$ 表示在图中如果任意子图的拓扑结构与 $Q_1$ 是同构的，且标签为 product 的点 $y$ 拥有属性 $type$ ="film"，那么标签为 person 的点的属性 $type$ 就会是 "producer"。
GFD $\varphi2 = Q_2[x,y,z](\phi \rightarrow y.name=z.name)$ 。该规则表明如果 city $x$ 位于 $y$ 和 $z$ 则 $y$ 和 $z$ 必须是同一个地点。注意： $y$ 和 $z$ 的 label 是通配符 "_"，所以可以同时匹配图 $G2$ 中的 $country$ 和 $city$ 两种 label。
GFD $\varphi3=Q_3[x,y](\phi \rightarrow false)$ 。该规则表明没有任何两个人可以互为对方的父母，即 $Q_3$ 是一个"非法"的结构。

GFD相关概念解释

基础概念

图（Graph）

对于一个有向图 $G=(V, E, L, F_A)$ ：

$V$ 表示实体点（后文中简称"点"）的有限集合。
$E\subseteq V\times V$ 表示实体关系（后文中简称"边"），其中 $(v, v')$ 是点 $v$ 到点 $v'$ 的边。
$L$ 表示 label（点或边的标识，可以理解为名字）。每一个点 $v\in V$ 都会属于一个 label： $L(v)\in \Theta$ ，每一个边 $e \in E$ 都会属于一个 label： $L(E)\in \Theta$ 。
对于每一个点 $v$ ， $F_A(v)$ 是一个元组 $(A_1=a_1,...,A_n=a_n)$ 。其中 $a_i$ 是一个约束， $A_i$ 是点 $v$ 的一个属性，写作 $v.A_i=a_i$ （即，实体点 $v$ 的属性 $A_i$ 的具体值为 $a_i$ ）。并且当 $i \neq j$ 时 $A_i \neq A_j$ 。

图模式（Graph patterns）

一个图模式是一个图 $Q_{[\bar{x}]} = (V_Q, E_Q, L_Q, \mu)$ 。

$V_Q$ （或者 $E_Q$ ）是一个点（或者边）模式的集合。
$L_Q$ 是一个函数，为每一个点 $u\in V_Q$ （或者边 $e \in E_Q$ ）分配一个 label $L_Q(u)$ （或者 $L_Q(e)$ ）。我们允许 $L_Q(u)$ 和 $L_Q(e)$ 使用通配符 '_'。
$\bar{x}$ 是一系列的变量。
$\mu$ 是一个从 $\bar{x}$ 到 $V_Q$ 的双射映射，它为 $V_Q$ 中的每个节点 $v$ 分配一个不同的变量。对于 $x \in \bar{x}$ ，当语义确定的时候，我们会等价地使用 $\mu(x)$ 和 $x$ 。

图模式匹配（Pattern matching）

对于标签 $l$ 和 $l'$ ，如果 $l \in \Theta$ 并且 $l'$ 是 '_'，我们写作 $l \prec l'$ 。如果 $l \prec l'$ 或者 $l=l'$ ，则我们写作 $l\preceq l'$ 。

模式 $Q$ 在图 $G$ 中匹配（match）是指一个 $G$ 的一个子图 $G'=(V', E', L', F'_A)$ 与 $Q$ 是同构的。即存在一个 $V_Q$ 到 $V'$ 的双向映射函数 $h$ ， $h$ 满足：

对于每一个点 $u \in V_Q$ , $L'(h(u)) \preceq L_Q(u)$ 。
$e=(u, u')$ 是一个 $Q$ 中的边，当且仅当 $e'=(h(u), h(u'))$ 是 $G'$ 中的一条边并且 $L'(E') \preceq L_Q(e)$ 。

图中的函数依赖（Functional Depandecies for Graphs）

一个图的函数依赖（GFD）写作 $Q[\bar{x}](X \rightarrow Y)$ ，其中：

$Q[\bar{x}]$ 是一个图模式，被称为 $\varphi$ 模式。
$X$ 和 $Y$ 是 $\bar{x}$ 的两个（可能是空的）属性的集合。

显然， $\varphi$ 是两个约束的组合：

模式 $Q$ 约束的拓扑结构。
$X \rightarrow Y$ 指定的属性依赖关系。

这里 $Q$ 指定了 $\varphi$ 的范围，使得 $X \rightarrow Y$ 只强加给 $Q$ 的匹配项。

语义表述（Semantics）

当 $h(\bar{x})$ 满足其集合 $X$ 中所有属性约束，我们记作 $h(\bar{x}) \models X$ 。如果 $h(\bar{x})\models X$ 可以推出 $h(\bar{x}) \models Y $，我们记作 $h(\bar{x})\models X \rightarrow Y$ 。

一个图 $G$ 满足 GFD $\varphi$ ，表示为 $G \models \varphi$ 。如果 $Q$ 的所有 $h(\bar{x})$ 都在 $G$ 中找到匹配， $h(\bar{x}) \models X \rightarrow Y$ 。图 $G$ 满足一个集合 $\Sigma$ 的 GFDs，记作 $G \models \Sigma$ ，如果所有的 $\varphi \in \Sigma, G \models \varphi$ 。

想要得知是否 $G \models \Sigma$ ，我们需要检查 $Q$ 在 $G$ 中的所有匹配。更多的，我们考虑无模式图，所以：

对于 $X$ 中的 $x.A = c$ ，如果 $h(x)$ 没有属性 $A$ ，则 $h(\bar{x})$ 满足 $X \rightarrow Y$ 。确实，点 $h(x)$ 并不需要拥有属性 $A$ 因为图没有模式。相反的，如果 $x.A=c$ 在 $Y$ 中并且 $h(\bar{x}) \models Y$ ，则根据满足性定义 $h(x)$ 必须拥有属性 $A$ 。对于 $x.A=Y.b$ 来说也是一样的。
当 $X$ 是 $\phi$ 时，对于 $Q$ 的任意匹配 $h(\bar{x})$ 都有 $h(\bar{x}) \models X$ 。当 $Y=\phi$ 时， $Y$ 始终为真， $\varphi$ 是平凡的。

显然，如果一个 $Q$ 的匹配 $h(\bar{x})$ 在 $G$ 中违反 $X \rightarrow Y$ ，例如 $h(\bar{x}) \models X$ 。但是 $h(\bar{x}) \not\models Y$ ，则由 $h(\bar{x})$ 导致的子图不一致，例如它的实体点有不一致性。

正向和负向（Positive and negative）

只有两种 GFDs $\varphi$ 是负向的：

当 $X=\phi$ 时，即 $\varphi$ 具有形式 $Q[\bar{x}](\phi \rightarrow false)$ 。这表明图模式就是不合理的。
当 $X \not = \phi$ 时，图模式和属性结合是不一致的。图 1.1 中 $\varphi1$ 和 $\varphi2$ 是正向， $\varphi3$ 是负向，因为图模式本身不合理。