7. 顺序的 GFD 发掘(SEQUENTIAL GFD DISCOVERY)

我们将时间顺序的 GFD 发掘算法记作: SeqDisGFD.

这里面包含两个问题:

1. SeqDis: 给定 $G$, $k$ 和 $\sigma$, 发现一个 k-bounded 的, 具备 $\sigma$ 频繁的 GFDs 集合 $\Sigma$.
2. SeqCover: 给定 $\Sigma$, 如何计算它的一个覆盖 $\Sigma_c$.

这两个问题我们将分别在 7.1 和 7.2 两节中讨论.

7.1 Sequential GFD Mining

如果使用暴力枚举算法, 首先根据传统图挖掘算法枚举出图 $G$ 中所有频繁模式 $Q$, 然后通过增加属性来生成 GFDs. 但是这种枚举 k-bounded GFDs 的方法在图 $G$ 非常大的时候代价很大.

为了降低代价, SeqDis 算法将这两个步骤合并为一个, 可以尽早地淘汰不感兴趣的 GFDs.

算法在 $k^2$ 次迭代中运行. 对于每个迭代 $i$, 发现并存储所有的大小为 $i$ (有 $i$ 条边)且 $\sigma$ 频繁的最小 GFDs 在 $\Sigma_i$ 集合中. 在最初的迭代中, 初始化一个 GFD 生成树 $T$, 存储只包含单点的模式的频繁 GFDs. 之后通过两个方向的扩展来扩展这个树:

1. 垂直扩展: 扩展模式 $Q$.
2. 水平扩展: 生成依赖 $X \rightarrow Y$.

每次迭代 $i(0<i<k^2)$, SeqDis 生成并证实 GFD 的候选项, 并填充在树 $T$ 的第 $i$ 层. 具体的操作为下面的两个步骤:

1. 模式证实.

   SeqDis 算法先进行垂直扩展. 在 $T$ 的第 $i$ 层生成一个新的图模式. 而每个图模式 $Q'$ 都是由第 $i-1$ 层的模式 $Q$ 通过扩展一条边(或者一条边和一个新点)得到的. 然后通过模式匹配找到第$i$层所有模式的匹配.

2. GFD 验证.

   算法随后进行水平扩展, 将一组属性与 $T$ 的第 $i$ 层上新验证的图形模式关联起来，以生成一组 GFD 候选项. 对于每一组候选项, 执行 GFD 验证去找到 $\Sigma_i$ 中的 GFDs, 即第 $i$ 层上满足 $G$, 并且是频繁的, 并且是最小的 GFD. 验证过程一致持续到第 $i$ 层的模式相关的所有的GFD候选项都被验证过.

这两个步骤不断迭代知道没有新的 GFDs 可以被生成, 或者所有的 k-bouned GFDs 都被遍历过.

接下来详细介绍垂直扩展和水平扩展, 算法的核心就是如何维持用来保存 GFD 候选项的生成树.

7.1.1 生成树

树 $T=(V_T, E_T)$ 控制着 GFD 候选项的迭代.

1. 每个在 $T$ 的第 $i$ 层的点 $v \in V_T$ 都存储着一个元组 $(Q[\bar{x}], lvec)$. 其中:

   1. $v.Q[\bar{x}]$ 是一个拥有 $i$ 个边的图模式.
   2. $v.lvec$ 是一个向量, 每个条目 $levc[l]$ 存储着一个以属性 $l$ 为根的属性树. 此时, $l$ 是 $x.A=c$ 或者 $x.A=y.B$, 其中 $x,y \in \bar{x}$, 且 $A,B$ 是 $\Gamma$ 中的属性, $c$ 是 $G$ 中的常量.

   每个第 $j$ 层的点的 $levc[l]$ 是一个属性集合 $X$, 使得 $Q[\bar{x}](X \rightarrow l)$ 是一个 GFD 的候选项. 对于一个属性 $l'$ 来说, 如果 $X_1 =X_2 \cup {l'}$, 则 $v.levc[l]$ 中有一个边 $(X_1, X_2)$.

2. 每个点 $v(A[\bar{x}], lvec)$ 拥有一个边 $(v, v') \in E_T$ 连接到另一个点 $v'(Q'[\bar{x}], lvec')$ 如果 $Q'$ 是由 $Q$ 扩展了一条单边形成的.

图 3.1: GFD 生成树

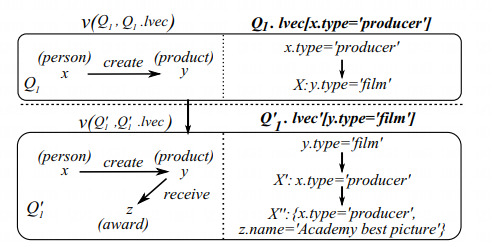
上图就是一棵 GFD 生成树 $T$, 展示了前文中提到过的两个 GFD, 分别是:

1. GFD $\varphi_1= Q1[x,y](y.type = film \rightarrow x.type =producer)$.
2. GFD $\varphi_4= Q'1[x,y,z]({x.type = producer,z.name =Academy \ best \ picture} \rightarrow y.type = film)$.

该生成树就只有两个节点，第一层的节点存储了 $v(Q_1,Q_1.lvec)$，其中 $Q_1$ 是节点左边展示的图模式, $Q_1.lvec$ 则是一个以 $x.type=producer$ 为根的树，相当于将 $\varphi_1$ 的函数依赖存储到一棵树. 第二层的节点存储了 $v(Q_1',Q_1'.lvec)$，而 $Q1'.lvec$ 以 $y.type=film$ 为根节点.

因为 $X''$ 是由 $X'$ 扩展一个属性得来的, 即 $X''=X'\cup {z.name=Academy\ best\ picture}$, 所以 $X'$ 和 $X''$ 之间存在一条边. 又因为 $Q_1'$ 是通过给 $Q_1$ 增加一条 $y\rightarrow z$ 的边得到的, 所以 $Q_1$ 到 $Q_1'$ 有一条边.

注

对于第 $i$ 层的 $\varphi=Q[\bar{x}](X \rightarrow l)$，长度 $\left|X\right|$ 最大为 $J=i \left|\Gamma\right| ( \left|\Gamma\right| + 1)$，其中 $\Gamma$ 由 $G$ 中的属性组成.

GFD 扩展

生成树 $T$ 通过不断执行下面的两个原子操作来生成新的 GFD 候选项.

垂直扩展($VSpawn$)

垂直扩展操作 $VSpawn(i)$ 会在第 $i$ 层通过在第 $i-1$ 层的 $v.Q$ 的基础上增加一条边 $e$ 来生成新的点 $v'.Q'$. 它通过增加边 $(v, v')$ 到 $T$, 使得 $T$ 在垂直方向上扩展.

显然 $VSpawn(i)$ 新增了一种图模式到 $T$, 当 $1 \le i \le k^2$. 对于第 $i-1$ 层的每一个 GFD $\varphi =Q[\bar{x}](X \rightarrow l)$ 来说, 它通过增加一条边到 $Q$ 来生成模式 $Q'$. 例如 图 3.1 中 $Q$ 进行垂直扩展, 增加边 $e=(y,z)$ 从而得到 $Q'$.

水平扩展($HSpawn$)

水平扩展通过属性和约束来生成字段. 具体来说, $HSpawn(i,j)$ 在 $T$ 中的第 $i$ 层, 字段树的第 $j$ 层执行. 例如 图 3.1 中 $HSpawn(2,j)$ 就是发生在第 2 层的新图模式上. $HSpawn(2,2)$ 通过增加 $z.name=Academy\ best\ picture$ 将 $level \ j=1$ 的 $X'$ 扩展到 $level \ j=2$ 的 $X''$.

剪枝

1. 当验证 $G\models Q[\bar{x}](X \rightarrow l)$ 时, 水平扩展 终止.
2. 当 $supp(Q,G) < \sigma$ 时, 垂直扩展 终止.

这两条策略可以保证 GFDs 发现在实际应用时的可行性.

引理 4

对于一个支持度高于 $\sigma$ 的 GFDs 覆盖集 $\Sigma_c$:

1. $\Sigma_c$ 不包含任何的平凡 GFD.
2. 对于任意的 $\varphi =Q[\bar{x}](X \rightarrow l)$, 如果 $G\models \varphi$, 则 $\Sigma_c$ 不包含 $\varphi'=Q[\bar{x}](X'\rightarrow l)$ 如果 $X\not \subseteq X$.
3. 如果一个 GFD $\varphi =Q[\bar{x}](X \rightarrow l)$ 满足支持度 $supp(Q,G)<\sigma$, 则 $\Sigma_c$ 不包含 $\varphi'=Q[\bar{x}](X'\rightarrow l)$ 如果 $Q\ll Q'$.

贡献者

• dingyuqi

变更历史

最后更新于: 查看全部变更历史

• aae8b-

  docs: update docs

  于 2024/11/21
• ae293-

  docs: add icon

  于 2024/11/22
• c2111-

  modify(docs): remanage folders and rename files

  于 2024/12/17

版权所有

版权归属：dingyuqi

本文链接：/paperNote/ym8cl2ch/

许可证：署名-非商业性-禁止演绎 4.0 国际 (CC-BY-NC-ND-4.0)